Differential Winch

2022 May 01Monthly MechanismDifferential Winch

Continuing our MonthlyMechanism series, let's look at the differential winch.

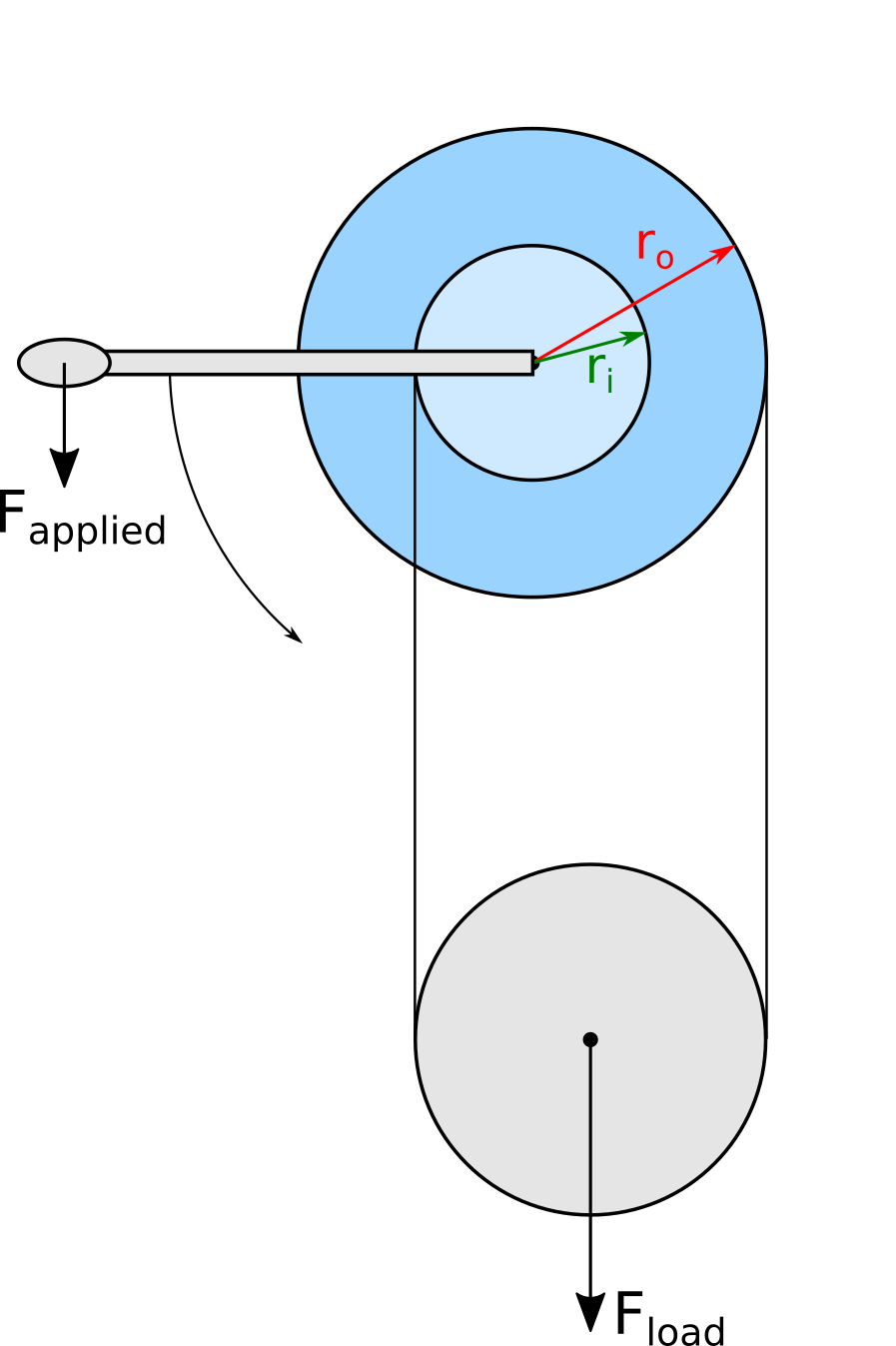
At its core are two reels of differing diameter on the same shaft, with the ends of a single cable attached to each. Between the reels the cable circuits a pulley, onto which a load is hung. Note that reels are wound in the same direction: the cable winding on the larger reel lies on the opposite side of the shaft from the cable unwinding from the smaller reel. Turning the reels by their common shaft leads to the simultaneous winding and unwinding of cable from the reels, though at differing rates from their differing diameters. These differing rates slowly change the length of cable between the reels, raising the load if the loop length is decreasing or lowering it when increasing.

Taking the end-view and summing moments about the shaft, the radii of the larger and smaller reels can be used to find the torque-load relationship as:

$T_{applied} = \frac{F_{load}}{2} (r_{outer} - r_{inner})$

Also needed is the change in load height per crank revolution:

$\frac{\Delta h }{\theta} = ro - ri$

Users generally want to know how 'hard' it will be to raise a given load, and as designers we want to understand how a differential winch compares to other options. Assuming crank operation, how hard to raise a load can be expressed as the ratio between the force applied to the crank handle and the weight of the load, with lower ratios being easier:

$\frac{F_{applied}}{F_{load}} = \frac{r_{outer} - r_{inner}}{2r_{handle}}$

If we take the outer and handle radii to be 1, we can compare several winches:

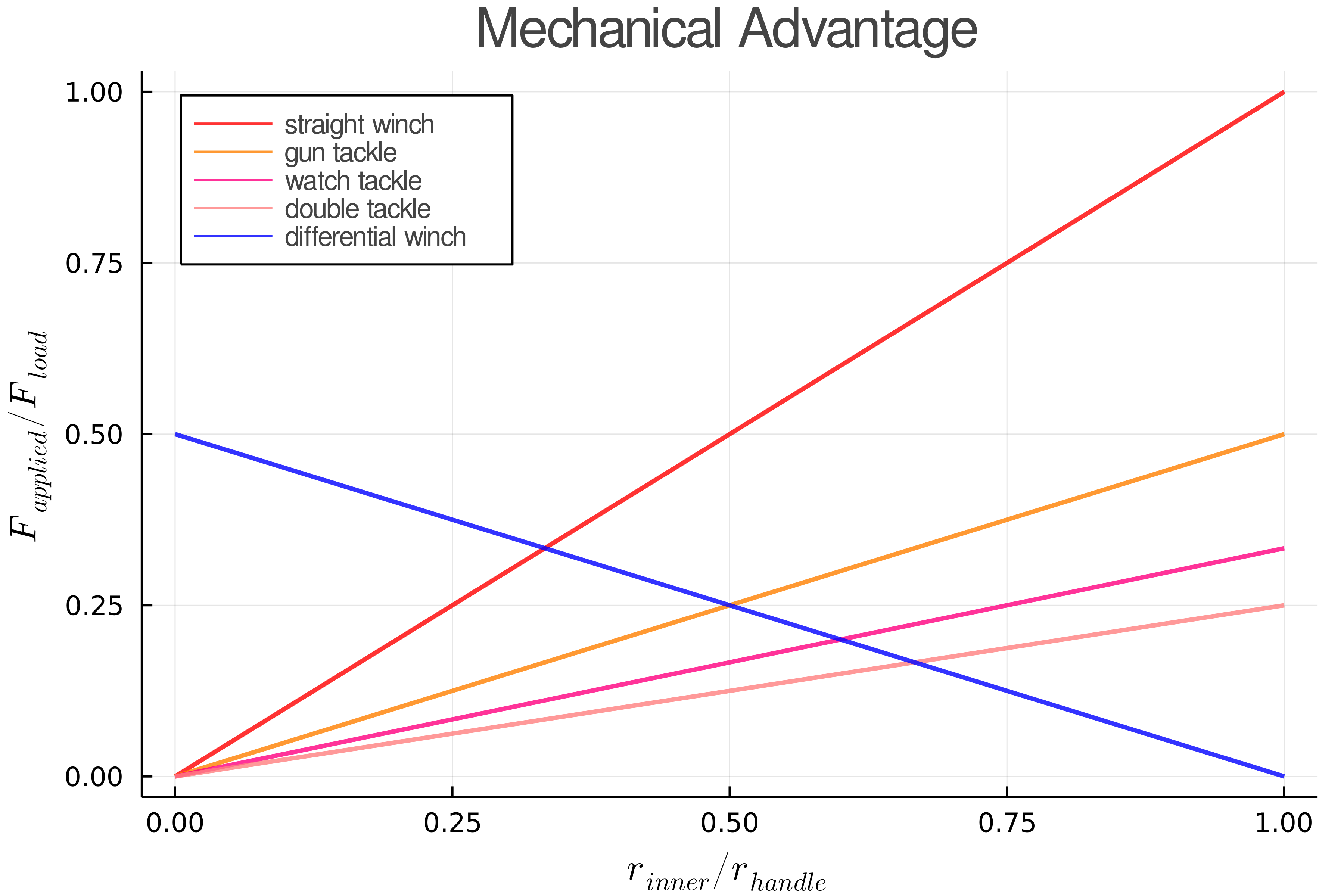
While decreasing the reel radius of the straight winch can yield significant advantage, it requires decreasing the reel and shaft diameters and hence their stiffness in torque and bending, increasing the likelihood that the shaft will break under a load. The differential winch, because it operates on the difference between the reel radii, can be used with arbitrarily large shafts and thereby avoid shaft breakage.

In Use #

One significant limitation of the differential winch is seen in the first picture, where the cable is shown as a single layer on the reel. In this design the distance the load may be lifted is limited by how much cable can fit on the reel before it is forced upon itself into a second layer. Additional layers away from the reel surface change the effective reel radius, thereby changing the reel radius.

A potentially larger problem from layering occurs in natural ropes and other cables with soft cross-sections, where layering rope upon itself under tension can lead to wedging between layers. This wedging, where an upper segment of rope is pulled between lower segments, can lead to irregular unwinding, especially at higher speeds. It can also disrupt subsequent layers, leading to greater wedging or to rope-crossing.

Have you seen or used a differential winch in-the-field? Take a picture and tag @mechanomy_ or send it our way. As always, comment on Twitter or LinkedIn, and subscribe to see next month's mechanism.

— Ben Conrad

---

• Next: Differential Belt Transmission
• Previous: Following Mechanomy