Compression Springs

2022 Nov 03Monthly Mechanism Julia Springs

In this #monthlyMechanism we write a simple Julia package to model compressive springs. Springs, of course, are a fundamental machine component and they are well-explained by mechanics. I'm using Fundamentals of Machine Elements as a reference, but many others exist.

The material and shape of a spring completely describe its function, which is summarized by the spring stiffness constant (spring rate) and calculated by

k = \frac{F}{\delta} = \frac{G d}{8 C^3 N_a (1 + \frac{1}{2C^2})} = \left[\frac{force}{distance}\right]

with $F$ being the applied force, $\delta$ deflection from the unloaded state, $G$ the material's shear modulus, $d$ the spring wire diameter, $N_a$ the number of free revolutions of the wire, spring index $C = D/d$ , and $D$ the coil diameter.

In Julia we start with a struct to hold these parameters:

struct CompressionSpring
  G::Unitful.Pressure
  d::Unitful.Length
  D::Unitful.Length
  Na::Real
  l0::Unitful.Length
end

I'm using the Unitful package to add unit handling to the parameters, which means that when instantiated $d$ can be given any length, from Ångströms to yards to centimeters

julia> a = 1u"angstrom" + 2u"yd" + 3u"cm"
18588000001//10000000000 m

and, given the vastly differing scales, is internally stored as a fraction until needed.

The spring constant can then be calculated:

function springIndex(s::CompressionSpring)
  return s.D/s.d
end

function springConstant(s::CompressionSpring)
  C = springIndex(s)  
  return s.G * s.d / ( 8 * C^3 * s.Na * ( 1+1/2/C) )
end

The spring parameters are significantly independent; given the wide variety of wire materials and diameters, and the ability to control coil diameter and number of turns, many spring sizes and constants are available.

As a quick example, here's how to model spring number 184 from WB Jones.

function jones184()
  G = 11.5e6u"psi" #zinc-clad "music wire" taken to be ASTM A228 high-carbon steel
  d = 0.016u"inch"
  D = 0.125u"inch" - d #convert from outer diameter to mean diameter
  Na = 11.9 #number of 'active' coils
  l0 = 0.75u"inch"

  return Springs.CompressionSpring(G, d, D, Na, l0)
end

The jones184() function holds the same information as a datasheet, and whereas datasheets are intended to be read and referred to, jones184() is meant to be used in calculations. For instance, we can calculate the force at a given displacement,

"""
  Calculates the spring force when deflected a distance `l` from the unstretched length.
  By convention this force is positive for compression springs and negative for extensional springs in tension.
  This function will issue a warning if the spring is compressed more than 85% of its length, where plastic 
  deformation is likely, or less than 15% where the force may be slightly inaccurate.
"""
function forceAt(s::CompressionSpring, l::Unitful.Length)
  f = springConstant(s) .* (s.l0-l) #as per convention, l0-l results in a positive force resisting the compression

  # See Shigley1996's definition on pg24.17
  if l/s.l0 < 0.15
    @warn "Spring likely compressed beyond linear region" s.l0 l f
  end
  if l/s.l0 > 0.85
    @warn "Spring only slightly compressed, calculated force possibly inaccurate" s.l0 l f
  end

  return f
end

f33 = Springs.forceAt(cs184, 0.33u"inch")

or plot the force/displacement curve,

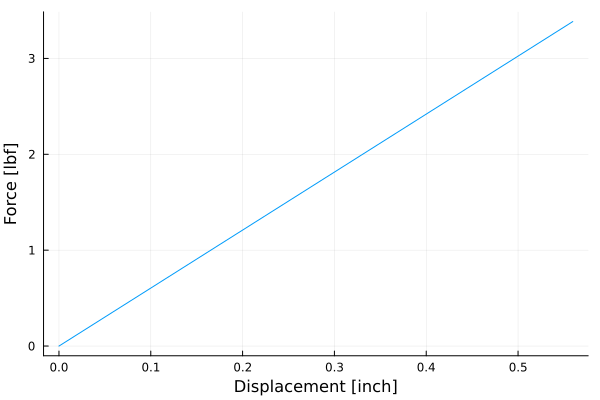
whose slope is the spring constant $k$ .

And that is it for this MonthlyMechanism. I didn't have time to get into spring non-linearities, plastic failure, resonances and surge, or selection criteria...maybe next month. Until then, share on Twitter or LinkedIn, and be sure to subscribe to see next month's mechanism.

— Ben Conrad

Next: RapidSlide Adjustable Wrench
Previous: Renishaw Equator